TeXに直接作図しよう!2
すでにTikZがインストールされていて,TeX文書ののコンパイルにはdvipdfmxを使うものと仮定して話を進めていきます。
パッケージを読み込もう
TikZをLaTeXで使うには,プリアンブルに次のように書く必要があります。
|
1 |
\usepackage{tikz} |
これでよさそうなのですが,これだけではdvipdfmxではうまく表示できません。画像関係の扱いはソフト固有の処理があるらしく,TikZに「dvipdfmxを使いますよ」と教えてあげなければなりません。そこで次の一行を加えます。
|
1 |
\def\pgfsysdriver{pgfsys-dvipdfmx.def} |
あるいは,次のようにgraphicxパッケージを読み込むのであれば上の一行は不要になります。
|
1 |
\usepackage[dvipdfmx]{graphicx} |
結局,
|
1 2 |
\def\pgfsysdriver{pgfsys-dvipdfmx.def} \usepackage{tikz} |
または
|
1 2 |
\usepackage[dvipdfmx]{graphicx} \usepackage{tikz} |
とプリアンブルに書くことで,TikZを使う準備が整いました。
必要に応じてTikZのライブラリーも読み込もう
\usepackage{tikz}だけではすべてのTikZの機能が使えません。この記事では必要に応じてまた説明しますが,例えば「calc」というTikZのライブラリーに含まれている機能が使いたければ,
|
1 |
\usetikzlibrary{calc} |
のようにプリアンブルに書く必要があります。
TikZコマンドの書き方
TikZのコマンド(\pathや\drawなど)はtikzpicture環境の中に記述します。tikzpicture環境の外に書くとエラーが出ます。
|
1 2 3 |
\begin{tikzpicture} %ここだよ!ここに書くんだよ!! \end{tikzpicture} |
\tikz{…}という書き方もあるのですが,基本的には,TikZのコマンドは必ずtikzpicture環境の中に記述するものだと思っておいてください。また,各行の最後にはセミコロン「;」を打ってください。ただし,行の最後というのは,改行の位置ではなく,ひとつのコマンドの最後という意味です。
点の座標(coordinate)のプリミティブな定め方を知る
TikZでは直線・曲線を引いたり,円を描いたりするときに,点の座標を指定します。点を指定するだけではまだ画面に何も表示させられませんが,最初が肝心ですので辛抱強く耐えてください。その指定方法には次のものがあります。
直交座標系(デカルト座標系:Cartesian coordinates)
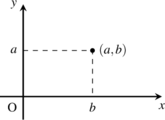
中学・高校の数学でもよく使う座標系なのでなじみがあるでしょう。右向きの上向きが正の向きです。スクリーン座標系(下向きが正)ではありません。x座標がa,y座標がbなら,
|
1 |
(a,b) |
と書きます。単位は付けても付けなくてもかまいません。付けなければ多分[cm]になります。
極座標(Polar coordinates)
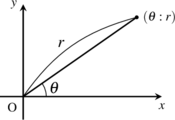
高校数学の最後のあたりで習い,しかも文系なら習わないかもしれない,でも大学入試でサッと使えるとたまに便利な,あの極座標です。原点Oからの距離がrで,x軸の正の向きとのなす角がθとなる点を
|
1 |
(θ:r) |
と書きます。高校で習う極座標の書き方は(r, θ)ですが,それとは違うので,注意しておいてください。また別の書き方として,
|
1 |
(canvas polar cs:angle = θ, radius = r) |
と書くこともできます。ただし,上の二つのいずれの場合もrには単位(px, cm など)をつける必要があります。(付けなくてもコンパイルは通りますが,直交座標に単位を明示しなかったときとは違う単位になります。)
直交座標で単位を明示しないときと同じ単位を使う場合は,
|
1 |
(xy polar cs:angle = θ, radius = r) |
とでき,rに単位をつける必要はありません。(逆に単位を付けるとコンパイルが通りません)
ある座標に名前をつける
数学でも「三角形ABCの重心をGとおく。」のように,点に名前をつけることがありますが,TikZでも点の座標に名前をつけると便利なことがあります。名前を付けたい座標を「(座標)」,名前を「name」とすると,
|
1 |
\path (座標) coordinate(name); |
というコマンドを書きます。この省略形の
|
1 |
\coordinate (name) at (座標); |
と書くこともできます。「(座標)」の部分には,直交座標(a,b)でも極座標(θ:r) or (xy polar cs:angle=θ, radius=r)でも,どんな指定方法の座標でも入ります。「name」は何文字でも構わないのですが,数学の慣習的に大文字のアルファベット一文字にすることが多いでしょうか。例を挙げますと,
|
1 |
\coordinate (O) at (0, 0); |
というコマンドを書いておけば,後ろの場所で「(0, 0)」の代わりに「(O)」と書くことができます。
プリミティブな相対座標
相対的な座標を用いる方法は他にもありますが,まずはtikzパッケージを読み込んだだけで使える相対座標を説明します。相対座標は《現在の座標》からの変位を,
|
1 |
++(変位) |
で表します。例えば,点Pがすでに与えられているとき,点Pからx軸方向にa, y軸方向にbだけ移動した点にQという名前を付けたければ,
|
1 |
\path (P) ++(a, b) coordinate(Q); |
と書けます。直交座標に限らす,極座標でも大丈夫です。これは,\pathコマンドの後ろが左から順番に解釈されるときに,まず(P)で《現在の座標》が点Pになり,次に++(a, b)で《現在の座標》を(a, b)分変位させ,最後にcoordinate(Q)で《現在の座標》にQという名前をつけているのだと考えることが出来ます。ですので,そのように解釈できない次のコードは不正です。
\coordinate (Q) at(P) ++(a, b);
「++(変位)」は《現在の座標》に《現在の座標》を変位させた後の座標を代入しますが,
|
1 |
+(変位) |
とすると《現在の座標》は変更されません。
例えば,「++(変位)」の場合,《現在の座標》が次々に移っていくので,
|
1 |
\draw (1,1) -- ++(1,0) -- ++(0,1) -- ++(-1,1); |
と同じ図形を相対座標を用いずに書くなら,
|
1 |
\draw (1,1) --(2,1) --(2,2) --(1,3); |

となりますが,「+(変位)」だと,
|
1 |
\draw (1,1) -- +(1,0) -- +(0,1) -- +(-1,1); |
と同じ図形を相対座標を用いずに書けば,
|
1 |
\draw (1,1) --(2,1) --(1,2) --(0,2); |

となります。これは《現在の座標》がずっと(1,1)のまま変わらないので,「+(変位)」では(1,1)から変位させたものが計算されるためです。
いずれまた,もっと複雑な点の指定方法を説明しますが,とりあえず次回は図形の描画から説明を始めましょう。